考研n阶导数的常见公式

考研数学：求解 n 阶导数

在数学中，求解函数的 n 阶导数是一个常见的问题，尤其在高等数学、微积分和工程数学等领域中经常遇到。下面我将简要介绍如何计算一个函数的 n 阶导数。

1. 一阶导数（一阶导数也称为一次导数）

一阶导数表示函数在某一点的变化率，通常用 \( f'(x) \) 或 \( \frac{df}{dx} \) 表示。它可以通过以下公式求得：

\[ f'(x) = \lim_{h \to 0} \frac{f(x h) f(x)}{h} \]

其中，\( h \) 是一个趋近于零的数。

2. 二阶导数（二阶导数也称为二次导数）

二阶导数表示一阶导数的变化率，也即函数曲线的曲率，通常用 \( f''(x) \) 或 \( \frac{d^2f}{dx^2} \) 表示。它可以通过对一阶导数再次求导得到：

\[ f''(x) = \frac{d}{dx}[f'(x)] \]

3. n 阶导数

类似地，对于任意正整数 \( n \)，函数的 \( n \) 阶导数可以通过对 \( (n1) \) 阶导数再次求导得到。一般地，\( n \) 阶导数表示为 \( f^{(n)}(x) \) 或 \( \frac{d^nf}{dx^n} \)。

求解方法

对于给定的函数 \( f(x) \)，我们可以采用以下步骤来求解其 n 阶导数：

1. 计算一阶导数 \( f'(x) \)。

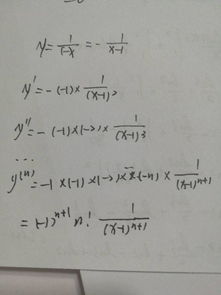
2. 根据需要，计算二阶导数 \( f''(x) \)，或者依次求解更高阶的导数，直到得到所需的 \( n \) 阶导数。

示例

让我们以一个简单的例子来说明如何求解一个函数的 \( n \) 阶导数：

假设我们有一个函数 \( f(x) = x^3 2x^2 3x 4 \)，我们要计算其二阶导数 \( f''(x) \)。

1. 计算一阶导数 \( f'(x) \)。对 \( f(x) \) 求导得到 \( f'(x) = 3x^2 4x 3 \)。

2. 再对 \( f'(x) \) 求导，得到二阶导数 \( f''(x) \)。对 \( f'(x) \) 求导得到 \( f''(x) = 6x 4 \)。

因此，函数 \( f(x) \) 的二阶导数 \( f''(x) \) 为 \( 6x 4 \)。

总结

求解函数的 \( n \) 阶导数是微积分中的一个重要概念，它在数学和工程等领域中都有广泛的应用。通过逐次求导，我们可以得到函数在某一点的高阶导数，从而更深入地理解函数的性质和行为。

希望这个简要的介绍能够帮助你理解如何求解函数的 \( n \) 阶导数。如果你有任何疑问或需要进一步的解释，请随时提出。